上海西门子6AV2125-2DB23-0AX0
上海西门子6AV2125-2DB23-0AX0上海西门子6AV2125-2DB23-0AX0
 | 6AV2125-2DB23-0AX0 SIMATIC HMI KTP400F Mobile 带集成式确认按钮, 急停开关, 触摸和按钮操作, 4" 宽屏 TFT 显示屏, PROFINET 接口, 可项目组态的*低版本 WinCC Comfort V13 Sp1,带有 HSP |
 | 6AV2125-2DB23-0AX0 SIMATIC HMI KTP400F Mobile 带集成式确认按钮, 急停开关, 触摸和按钮操作, 4" 宽屏 TFT 显示屏, PROFINET 接口, 可项目组态的*低版本 WinCC Comfort V13 Sp1,带有 HSP |
相量法是分析正弦交流电路的一种简单易行的方法。它是结合数学理论与电路理论而建立起来的一种系统方法。正弦量的相量表示法是指:一个正弦量的瞬时值可以用一个旋转矢量在纵轴上的投影值来表示。矢量,简单来说就是既有大小又有方向的量。
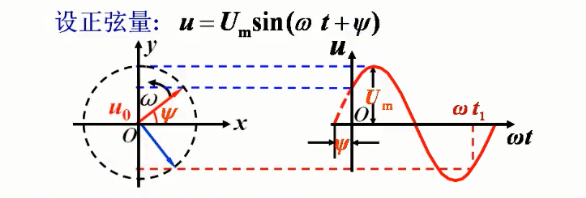
图30-1
如上图30-1所示,设正弦量u=Umsin(ωt Ψ),其波形图如图右所示,以该正弦量的幅值Um作为旋转矢量的长度(即虚圆的半径),初相角Ψ作为旋转矢量与横轴的夹角并以此作为起点,使旋转矢量以角速度ω按逆时针方向在直角坐标轴上旋转,对于某一时刻ωt1,该旋转有向线段在纵轴上的投影(虚线与y轴的交点)显然就是对应时刻正弦量的瞬时值,这就是正弦量的相量表示。

另外,回顾上次我们所学的周期与角速度的关系ωT=2π,以图30-1为例,想象一下,当旋转矢量旋转一周期(2π)后,我们可以很快发现,它又回到了初始的位置,对应波形图,此时的正弦量的值恰好也是等于其初始时的值,不同的只不过是时间罢了。
如下图30-2所示,正弦量u、i等的相量书写方式是在对应电量的大写字母U(或Um)、I(或Im)上加“·”(点)符号表示,若正弦量的幅度用大值表示,则对应电量的大写字母应加下角标“m”。在实际应用中,正弦量的幅度一般都是采用有效值表示,即没有下角标“m”。相量中的“·”(点)号即是表示与正弦量相关的复数身份,以区别于一般的复数,同时也表示区别于正弦量的幅值或有效值。相量符号本身就包含幅度和相位信息。
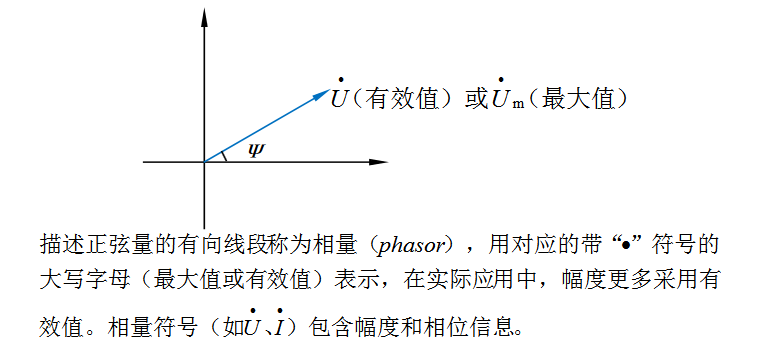
图30-2
正弦量的相量表示,实质上就是用复数表示正弦量,即正弦量的对应相量是一个复数。所以,复数及其运算是应用相量法的数学基础,我们要懂得相量,就必须要懂得复数。所谓复数,实质上是由实数和虚数组成的一对数,实数包括有理数和无理数。
一个复数有多种表示形式。复数F的代数形式为F =a jb,其中j为虚数单位。虚数理解起来可能比较困难,但这并不影响我们学习复数,在此我也不对虚数展开讲解。
另外,j还可以表示为旋转90°因子±j,即±j=cos90°±sin90°。j作为旋转90°因子在与有功和无功、电阻和电抗、容抗和感抗相关正弦交流电路的相量分析中带来很大的便利。某相量乘以 j,就是将该相量逆时针旋转90°,某相量乘以-j,就是将该相量顺时针旋转90°。
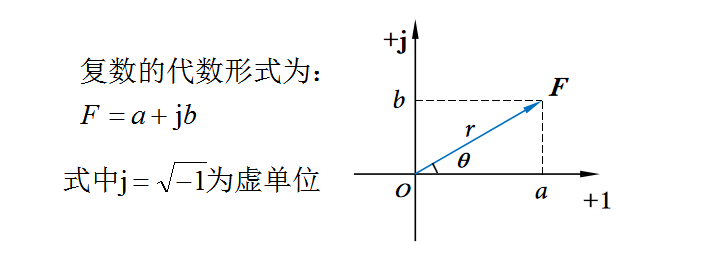
图30-3
复数F的代数形式F =a jb中,a称为复数F的实部,b称为复数F的虚部。复数在复平面上是一个坐标点,常用原点至该点的向量表示,如图30-3所示,其中r为复数的模(值),表示为|F |,θ为复数的辐角,即θ=argF ,θ可以用弧度或度表示。

在这里说明一下,向量和相量是不同的,相量是电子工程学中用以表示正弦量大小和相位的矢量;而向量是在数学中表示具有大小和方向的量,与之对应的没有方向的数量叫标量。
上文提到,一个复数是有多种表示形式的,除了其代数形式,还有三角形式、指数形式和极坐标形式。
如下图30-4所示,根据复数F在复平面上的表示,可以得到复数F的三角形式。结合复数F的代数形式,|F |和θ与a和b之间的关系如图30-4中所示。在一些书面上,复数F的实部还会表示为Re[F ],即a =Re[F ];虚部表示为Im[F ],即b =Im[F ]。

图30-4
另外,复数F的指数形式和极坐标形式如下图30-5所示。其中ejθ=cosθ sinθ是欧拉公式的表达式,这是属于复变函数的知识,较为复杂,在此就不展开讲解啦。我们只需知道结论即可。极坐标和直角坐标都是二位坐标系统,相对于直角坐标系,极坐标系只有一条坐标轴叫极轴,其原点叫极点,如图30-5所示。

图30-5
综上,复数F的表示形式有F =a jb =|F |(cosθ sinθ)=|F |ejθ=|F |∠θ。这是在数学理论里的复数,而在电路理论中的复数表示的是正弦量的相量。
把数学领域的复数运用到电路领域,其实也很简单,只不过是将复数F符号用正弦量中各电气量对应的相量符号代替,如下图30-6所示。

图30-6

关于正弦量与相量,以下几点需要大家注意:
(1)相量只是表示正弦量,而不是等于正弦量。这是因为正弦量是一个变量,它是瞬时变化的,而相量只是一个有方向和大小的量,它代表的是正弦量在某一时刻的值。
(2)只有正弦量才能用相量表示,非正弦量不能用相量表示。这是因为相量本身就是为分析正弦交流电路而存在的。
(3)只有同频率的正弦量才能画在同一相量图上。
在上一次的学习中提到过,同频的正弦量之间的代数和,其结果仍为同频率的正弦量。也就是因为角频率的不变,所以在讨论研究同频率的正弦量时,可以不用考虑其角频率,只需研究其幅值和初相角的变化。
同理,在相量图上,因为各正弦量的频率相同,我们只需比较它们对应相量的模与辐角即可。
相量图其实就是把相量表示在复平面的图形,类似于图30-3中的复数F。如下图30-7为两个正弦量的相量图表示。从相量图中,我们可以很快的看出,正弦量u1与u2的关系。
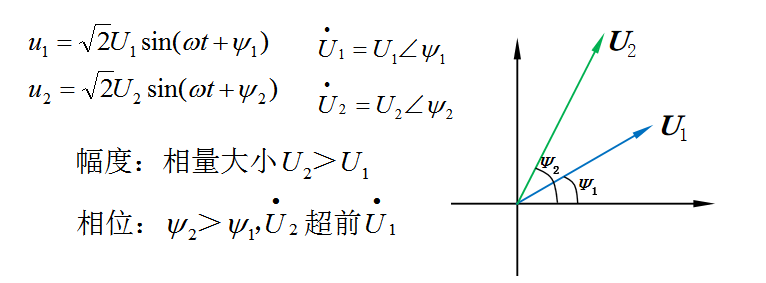
图30-7
复平面的直角坐标系有四个象限,显然相量在复平面上表示时可以在任一象限中,如下图30-7所示,当相量的实部和虚部取值不同时,其相量图会出现在不同的象限中。

当a、b均大于零时,相量在象限;当a小于零,b大于零时,相量在第二象限;
当a、b均小于零时,相量在第三象限;当a大于零,b小于零时,相量在第四象限。
另外,辐角Ψ取值范围为180°≥Ψ≥0°时,相量在、二象限;辐角Ψ取值范围为0°≥Ψ≥-180°时,相量在第三、四象限。
大家可以尝试画一下几种不同情况的相量图,以加深印象,这也方便大家在之后以相量图分析电路时能熟练运用。
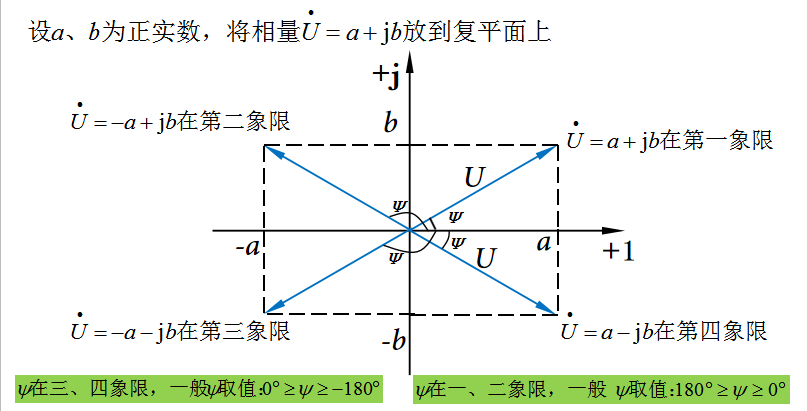
图30-8
正弦量的运算可以采用相量的加减乘除来实现,其本质就是复数的加减乘除。所以,关于相量的复数运算规则,其实就是复数的运算规则。
如下图30-9所示为相量的加减表示。相量的加减遵循平行四边形法则,即两个相量的相加,把其中一个相量沿另一个相量平移,使两相量首尾相连,得到的平行四边形的新相量(对角线)即为两者之和;

两个相量的相减如图30-9中的(2)所示,以被减数作为平行四边形的对角线,减数作为平行四边形的一条边,两者首尾相连得到平行四边形的另一条边即为两者之差。
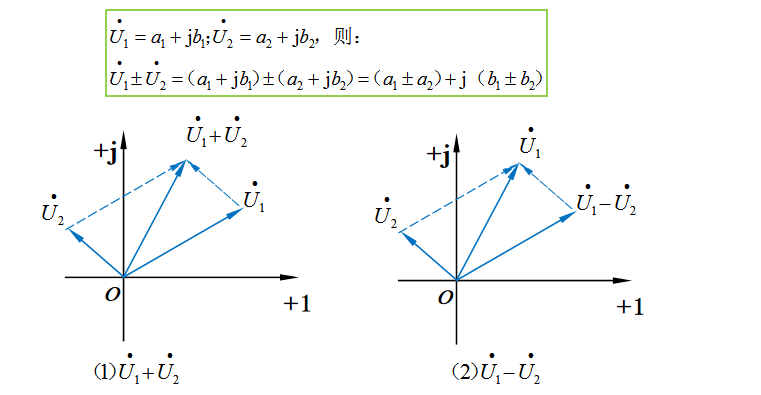
图30-9
相量的乘除如下图30-9所示,两个相量相乘,即把两者的有效值相乘得到积的有效值,把两者的初相角相加得到积的初相角;
两个相量相除,即把两者的有效值相除得到商的有效值,把两者的初相角相减得到商的初相角。相量的积和商的相量图大家可以自行尝试画一下,在这里我就不再作展示。
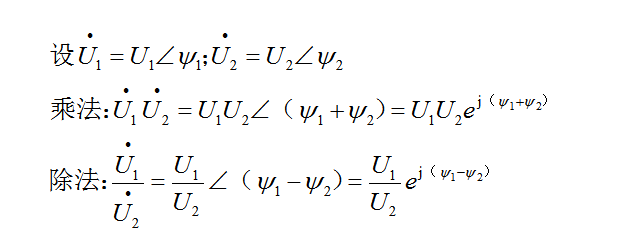
图30-10
| 6ES7214-1AG40-0XB0 | CPU 1214C DC/DC/DC,14输入/10输出,集成2AI |
| 6ES7214-1HG40-0XB0 | CPU 1214C DC/DC/Rly,14输入/10输出,集成2AI |
| 6ES7215-1BG40-0XB0 | CPU 1215C AC/DC/Rly,14输入/10输出,集成2AI/2AO |
| 6ES7215-1AG40-0XB0 | CPU 1215C DC/DC/DC,14输入/10输出,集成2AI/2AO |
| 6ES7215-1HG40-0XB0 | CPU 1215C DC/DC/Rly,14输入/10输出,集成2AI/2AO |
| 6ES7217-1AG40-0XB0 | CPU 1217C DC/DC/DC,14输入/10输出,集成2AI/2AO |
- 遵义西门子电源一级代理商 2023-11-04
- 西门子CPU模块222XPCN主机 2023-11-04
- 西门子CPU模块224XPCN AC/DC/RLY 2023-11-04
- 六盘水西门子交换机一级代理商 2023-11-04
- 西门子S7-1200模块可编程控制器 2023-11-04
- 贵阳西门子电机一级代理商 2023-11-04
- 贵州西门子触摸屏一级代理商 2023-11-04
- 西门子S7-1200模块/交换机模块 2023-11-04
- 铜川西门子S7-1200代理商 2023-11-04
- 西门子CPU供应224XPCN继电器模块 2023-11-04
- 深圳触摸屏6AV2125-2JB23-0AX0 2023-11-04
- 西门子S7-1500中央处理器CPU模块 2023-11-04
- 西门子CPU224XPCN晶体管模块 2023-11-04
- 巴中西门子一级代理商 2023-11-04
- 西门子S7-400模块CPU416F-3PN/DP 2023-11-04
联系方式
- 地址:上海 上海市松江区石湖荡镇塔汇路755弄29号1幢一层A区213室
- 邮编:201600
- 电话:15021292620
- 销售:颜娟
- 手机:15021292620
- 传真:021-33556143
- 微信:X15021292620
- QQ:2799536152
- Email:2799536152@qq.com